 このページを印刷する
このページを印刷する
- 先端技術研究所
世界初、1161次元の符号暗号を解読!
~10の48乗通りの候補が存在する前人未到の問題を、約375時間で成功!~
2021年1月14日
株式会社KDDI総合研究所
株式会社KDDI総合研究所(本社:埼玉県ふじみ野市、代表取締役所長:中村 元、以下「KDDI総合研究所」)は、暗号解読コンテスト「Challenges for code-based problems(注1)」において、1161次元の Syndrome Decoding in the Goppa-McEliece Setting(以下「SD」)問題を、世界で初めて(注2)解読しました。解読アルゴリズムの改良ならびに並列マルチスレッド環境に適した最適化を行い、解読処理の約250倍の高速化を達成しました。商用クラウドの8台の仮想PCでも、1台当たりの並列数を17,000,000とした解読を行うことで、10の48乗(=1京×1京×1京)通りの候補が存在し、総当たり方式による計算では1億年以上かかる(注3)1161次元のSD問題の解読を、約375時間で成功しました。本件に関連した研究成果について、2021年1月19日~22日にオンラインで開催される 「2021年暗号と情報セキュリティシンポジウム(SCIS 2021)」で発表を行う予定です。
公開鍵暗号(注4)技術はインターネットをはじめとする情報通信システムの安心・安全を支える基盤技術であり、ネットショッピングやICカードなどで日常的に利用されています。現在最も広く使用されているRSA暗号も公開鍵暗号方式であり、大きな数の素因数分解の困難性をその安全性の根拠としています。しかし近年、実用的な量子コンピュータの登場により、素因数分解が高速に計算できるようになり、今後は量子コンピュータに対しても安全性を確保できる公開鍵暗号方式が必要とされてきます。米国でも、アメリカ国立標準技術研究所が主導する耐量子暗号の標準化プロジェクト(NIST-PQC)において、次世代の公開鍵暗号の選定が進められています。
今回KDDI総合研究所が解読したSD問題は、係数、定数項および解が0と1のみで構成される多元連立1次方程式です。また、解における「1」の個数は問題ごとに与えられている定数以下である必要があります。この問題は量子コンピュータを用いても効率的に解読できないとされており、その難しさは、NIST-PQCの最終候補に選定されたClassic McEliece暗号を含む符号暗号(注5)の安全性の根拠となっています。安全な符号暗号を実現するためには、SD問題の次元(未知変数の個数)を高め、解読を困難にする必要がありますが、次元が大きすぎると暗号の処理時間が増大します。このため、安全性が確保される最適な次元を求めるために、高速な解法の研究が進められています。
本成果は、次世代公開鍵暗号として符号暗号を利用する際に、安全な次元の大きさを決めるための非常に重要な情報となります。KDDI総合研究所は、安心して利用できる情報通信システムの構築に貢献するため、引き続き解読アルゴリズムの高速化検討を進めるとともに、より高速で安全な次世代公開鍵暗号実現に向けた研究開発を推進していきます。
図:解読アルゴリズムの概要
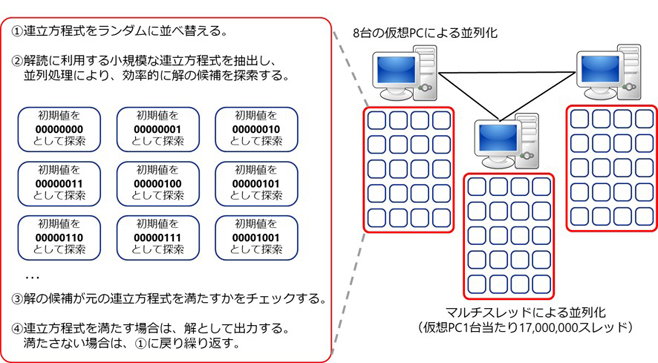
<KDDI総合研究所の取り組み>
KDDIとKDDI総合研究所は、経済発展と社会的課題の解決を両立する持続可能な生活者中心の社会「Society 5.0」の実現を加速する、2030年を見据えた次世代社会構想「KDDI Accelerate 5.0」を策定しました。両社は、ネットワーク、プラットフォーム、ビジネスの3レイヤの環境整備を進めると共に、3つのレイヤを支える先端技術となる7つの分野のテクノロジーと、それらが密接に連携するオーケストレーション技術の研究開発を推進します。
今回の成果は7分野のテクノロジーの中の「セキュリティ」に該当します。
(注1) フランス国立情報学自動制御研究所(INRIA)が主催する符号暗号に関する暗号解読コンテスト。2019年7月21日にウェブサイトが公開され、コンテストが開始された。KDDI総合研究所が解読したSD問題を含む計5種類の問題が出題され、世界中の暗号研究者が参加している。
Welcome to the code-based challenges webpage!
(注2)2021年1月10日時点
世界記録が掲載されたウェブサイト
Syndrome Decoding in the Goppa-McEliece Setting
(注3)解読アルゴリズムを利用せず、解となりうる全ての可能性を、2021年時点における世界最高性能のスーパーコンピューターで試した場合。
(注4)二つの鍵(AとA')を作成し、一方の鍵Aで暗号化し、もう一方の鍵A’で復号するという仕組み。自分あてに情報を送るための暗号化用の鍵(A)は世間に広く公開しておき(公開鍵)、 その鍵(A)を使って暗号化して送ってもらう。復号するためには、公開してある鍵ではないもう一方の鍵(A’)で復号する。この復号するための鍵(秘密鍵)は復号する本人しか知らないので、復号できるのは本人のみとなる。この二つの鍵は、数学的な関係があるので、関係のない他の鍵で復号することはできない。RSA暗号や楕円曲線暗号などが主流となっており、ネットショッピングにおける個人情報のやり取りなどに使われている。
(注5)SD問題など符号理論に関連する問題を安全性の根拠とする公開鍵暗号方式。次世代公開鍵暗号の有力な候補の一つで、現在最も広く使用されているRSA暗号よりも安全かつ高速な方式として期待されている。符号暗号は、シンプルな演算による暗号の処理が可能であり、かつ並列化による高速化も容易である。このため、特に処理能力に制約のあるIoT機器や組み込み機器などへの搭載が期待されている。
※ニュースリリースに記載された情報は、発表日現在のものです。 商品・サービスの料金、サービス内容・仕様、お問い合わせ先などの情報は予告なしに変更されることがありますので、あらかじめご了承ください。