 Print
Print
- Advanced Technology Laboratories
Breaking a world record: Solving 1,161-dimensional code-based cryptography
~A solution to an unprecedented problem with 10 to the power of 48 solution candidates, achieved in 375 hours. ~
January 14, 2021
KDDI Research, Inc.
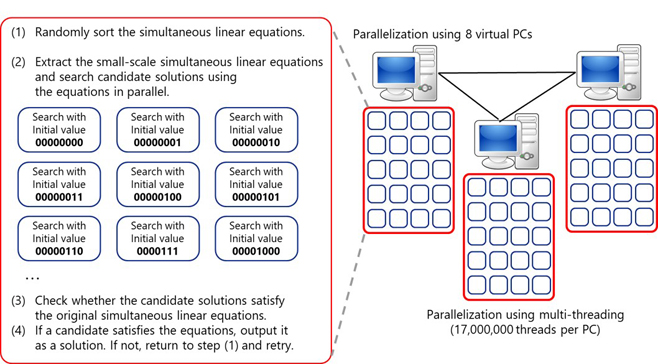
KDDI Research, Inc. (Head Office: 2-1-15 Ohara, Fujimino-shi, Saitama Prefecture; President & CEO: Hajime Nakamura) has succeeded in solving an 1161-dimensional Syndrome Decoding in the Goppa-McEliece setting,* within Challenges for Code-based Problems, a worldwide cryptanalysis competition. The solving program has been accelerated by a factor of 250 by improving the algorithm and optimization for parallel, multi-threaded environments. We have successfully solved the 1161-dimensional syndrome decoding problem (SDP), which has 10 to the power of 48 (one trillion to the power of four) solution candidates and would take more than 100 million years to solve using a brute force attack.(Note 1) Our solution took 375 hours, executing seventeen million parallel threads per PC and eight virtual PCs in a commercial cloud. The research results will be presented at the 38th Symposium on Cryptography and Information Security (SCIS 2021**) to be held online on January 19–22, 2021.
* Syndrome Decoding in the Goppa-McEliece setting
** The 38th Symposium on Cryptography and Information Security
Public-key cryptography (Note 2) is a fundamental technology that provides security for information and communication systems, including the Internet, and is routinely used for online shopping, IC cards, etc. RSA cryptography, which is the most widely used cryptography today, is also public-key cryptography, with security based on the difficulty of factorization problems. However, quantum computers can factor large integers and break RSA cryptography. Thus, new public-key cryptography that can protect against quantum computers is desired. The US National Institute of Standards and Technology (NIST) is leading a project to standardize post-quantum cryptography (NIST-PQC).
The SDP solved by KDDI Research is a multi-dimensional simultaneous linear equation whose coefficients, constant terms, and solutions consist of 0 and 1 alone. The number of 1’s in the solution must be less than or equal to a given constant. The SDP is considered to have no efficient solution, even with the use of quantum computers, and its difficulty is the secure basis of code-based cryptography (Note 3), including Classic McEliece, selected as a finalist for the NIST-PQC. Code-based cryptography needs to increase the dimension (number of unknown variables) of the SDP to guarantee security; however, processing time will increase unacceptably if the dimension is too large. Therefore, we have studied the computational complexity of SDP to find an optimal dimension that ensures the security and performance of code-based cryptography.
■ Overview of the program of SDP
(Note 1) Solving time based on checking all the possible candidates without using any solving algorithm, using the world's most powerful supercomputer as of 2021.
(Note 2) Cryptography contains two keys (A and A'), key A is used to encrypt, and A' is used to decrypt. Key A is made available to the public (public key), and the message is encrypted using the key and sent to the key owner. Key A' is securely stored by the owner (private key), and only the owner can use the key to decrypt ciphertexts. These two keys have a mathematical relationship, and no key other than key A' can decrypt the ciphertexts encrypted with key A. RSA cryptography and elliptic curve cryptography are the most commonly used approaches to public-key cryptography and are used to exchange personal data during online shopping.
(Note 3) Public-key cryptography, where the basis of security constitutes problems related to coding theory, including SDP. This is one of the post-quantum cryptography candidates and is expected to be more secure and faster than RSA cryptography. Code-based cryptography consists of simple operations and can easily be parallelized to increase performance; thus, it is expected to be used in resource-constraint devices, including IoT-related and embedded devices.
※The information contained in the articles is current at the time of publication.Products, service fees, service content and specifications, contact information, and other details are subject to change without notice.